แนวข้อสอบ SAT Math อัปเดตปี 2025 ตัวอย่างโจทย์ SAT ออกบ่อยต้องรู้

น้องคนไหนกำลังหาข้อมูลสำหรับเตรียมตัวไปสอบ SAT Math เพื่อเอาคะแนนไปยื่นเข้าเรียนต่อคณะในฝัน วันนี้พี่กริฟฟินจะพาทุกคนไปดูแนวข้อสอบ SAT Math ฉบับอัปเดตปี 2025 พร้อมตัวอย่างโจทย์แต่ละหัวข้อ และแจกตัวอย่างข้อสอบพร้อมเฉลยให้ลองไปฝึกทำกันแบบจัดเต็ม!

SAT Math คืออะไร?

ถ้าใครยังไม่ทราบว่าข้อสอบ SAT Math คืออะไร พี่กริฟฟินก็ขออธิบายให้เข้าใจง่าย ๆ ว่าเป็นข้อสอบวัดความถนัดทางคณิตศาสตร์ในระดับมัธยมปลายที่มหาวิทยาลัยหลายแห่งทั้งในไทยและทั่วโลกให้การยอมรับว่าเป็นคะแนนมาตรฐานที่สามารถใช้ยื่นเข้าศึกษาต่อในระดับปริญญาตรีได้ โดยที่แต่ละคณะวิชาและมหาวิทยาลัยก็จะมีการกำหนดเกณฑ์คะแนนที่ต่างกันออกไป

แนวข้อสอบ SAT Math สอบอะไรบ้าง มีกี่ข้อ พร้อมตัวอย่างข้อสอบ

ในส่วนของตัวข้อสอบ SAT Math ก็จะเน้นไปที่การวัดความรู้และความถนัดทางทางคณิตศาสตร์ รวมไปถึงวัดความสามารถคำนวณและการใช้งานตรรกะต่าง ๆ ของผู้สอบ ซึ่งจะมีทั้งข้อสอบที่เป็นแบบปรนัยหรือข้อสอบแบบเลือกตอบ (Choice) และข้อสอบแบบ Student Produced Responce ที่ผู้สอบจะต้องเขียนคำตอบลงใน Answer Sheet ด้วยตัวเอง โดยในปัจจุบันข้อสอบ Digital SAT ได้ปรับระบบให้สามารถใช้งานเครื่องคิดเลขบนแอปพลิเคชันในการคำนวณข้อสอบได้อย่างสะดวกยิ่งขึ้น สามารถแบ่งแนวข้อสอบ SAT Math ออกเป็นทั้งหมด 4 หัวข้อ ตามเนื้อหาการสอบ ดังนี้

1. Algebra (พีชคณิต)

ข้อสอบในหัวข้อพีชคณิต จะมีโจทย์อยู่ที่ 13 – 15 ข้อ คิดเป็น 35% ของข้อสอบทั้งหมด เน้นวัดความสามารถด้านการคิดวิเคราะห์และแก้ไขโจทย์ปัญหาทางคณิตศาสตร์ โดยจะประกอบไปด้วย 5 หัวข้อย่อย ได้แก่

• สมการเชิงเส้น 1 ตัวแปร (Linear Equations in 1 Variable)

ตัวอย่างคำถาม

If f(x) = x + 7 and g(x) = 7x, what is the value of 4f(2) − g(2)?

A) −5

B) 1

C) 22

D) 28

ข้อนี้ตอบ C เพราะ f(2) สามารถหาค่าได้จากการแทนค่า x ด้วย 2 ซึ่งในสมการกำหนดว่า f (x) = x + 7

เมื่อแทนค่า f (2) = 2 + 7 หรือ f (2) = 9 ค่าของ g(2) ก็จะสามารถหาได้โดยการแทนค่า x ด้วย 2 ในสมการที่กำหนด g(x) = 7x ซึ่งจะได้ g(2) = 7(2) หรือ g(2) = 14

ค่าของนิพจน์ (Expression) 4f (2) − g(2) สามารถหาได้โดยการแทนค่าที่สอดคล้องกันในนิพจน์

ซึ่งจะได้ 4(9) − 14 นิพจน์นี้เทียบเท่ากับ 36 − 14 หรือ “22” นั่นเอง

• สมการเชิงเส้น 2 ตัวแปร (Linear Equations in 2 Variables)

ตัวอย่างคำถาม

The y-intercept of the graph of y = −6x − 32 in the xy-plane is (0, y). What is the value of y ?

ข้อนี้ตอบ -32 เนื่องจากหากกำหนดให้ค่าตัดแกน y ของกราฟเป็น y = −6x − 32 คือ (0, y)

เมื่อแทนค่า x ด้วย 0 ในสมการนี้ จะได้ y = −6(0) − 32 หรือ y = −32

ดังนั้นค่า y ที่สอดคล้องกับค่าตัดแกน y ของกราฟของ y = −6x − 32 ในระนาบ xy คือ −32 (ข้อนี้เป็นการตอบแบบฝนข้อลงในกระดาษคำตอบ)

• ฟังก์ชันเชิงเส้น (Linear Functions)

ตัวอย่างข้อสอบ

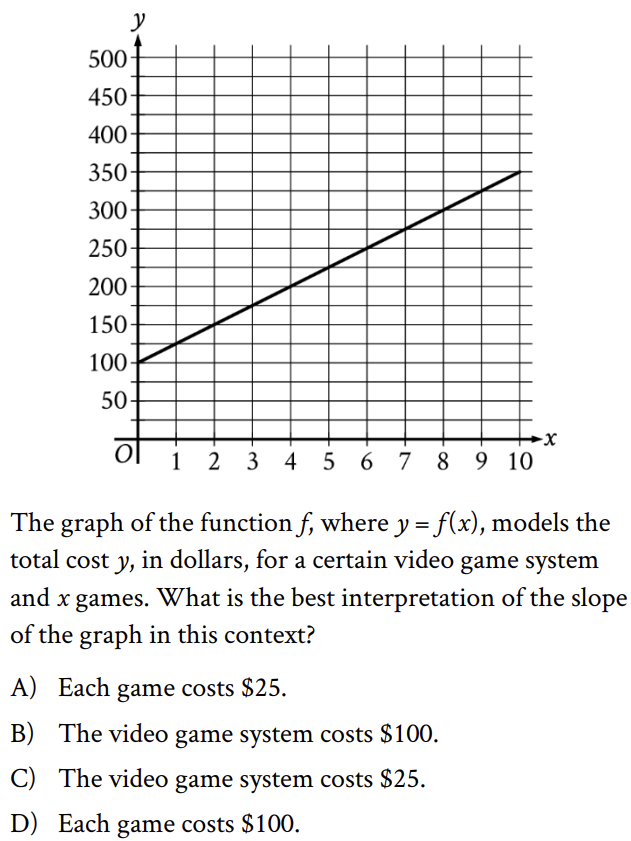
ข้อนี้ตอบ A เพราะกราฟในโจทย์เป็นกราฟเส้นตรงที่กำหนดให้ค่าความชันของ y

มีการเปลี่ยนแปลงเมื่อค่า x เพิ่มขึ้นครั้งละ 1 หน่วย ในโจทย์นี้กำหนดให้ y แทนต้นทุนรวมที่เป็นเงินดอลลาร์ ส่วน x แทนจำนวนเกม เมื่อจำนวนเกมเพิ่มขึ้น ต้นทุนก็เพิ่มขึ้นตามไปด้วย ดังนั้นความชันของกราฟจึงแสดงถึงต้นทุนที่เป็นเงินดอลลาร์ต่อเกม ซึ่งจากกราฟแสดงให้เห็นว่าเมื่อค่าของ x เพิ่มขึ้นจาก 0 เป็น 1 ค่าของ y จะเพิ่มขึ้นจาก 100 เป็น 125

ดังนั้น ความชันคือ 25 หรือต้นทุนของเกมแต่ละเกมจึงมีค่าเท่ากับ 25 ดอลลาร์นั่นเอง

• ระบบสมการเชิงเส้นสองตัวแปร (Systems of 2 Linear Equations in 2 Variables)

ตัวอย่างข้อสอบ

Store A sells raspberries for $5.50 per pint and blackberries for $3.00 per pint. Store B sells raspberries for $6.50 per pint and blackberries for $8.00 per pint. A certain purchase of raspberries and blackberries would cost $37.00 at store A or $66.00 at store B. How many pints of blackberries are in this purchase?

A) 12

B) 8

C) 5

D) 4

ข้อนี้ตอบ C เพราะโจทย์กำหนดว่าร้าน A ขายราสเบอร์รี่ไพนต์ละ 5.50 ดอลลาร์ และขายแบล็กเบอร์รี่ไพนต์ละ 3.00 ดอลลาร์ ส่วนร้าน B ขายราสเบอร์รี่ในราคา 6.50 ดอลลาร์ต่อไพนต์ และแบล็กเบอร์รี่ในราคา 8.00 ดอลลาร์ต่อไพนต์

เมื่อซื้อราสเบอร์รี่และแบล็กเบอร์รี่ที่ร้าน A เป็นจำนวน 37.00 ดอลลาร์ และซื้อที่ร้าน B อีก 66.00 ดอลลาร์

โดยใช้ r แทนจำนวนไพนต์ของราสเบอร์รี่ และ b แทนจำนวนไพนต์ของแบล็กเบอร์รี่ ของร้าน A

มีสมการดังนี้ 5.50r + 3.00b = 37.00 ส่วนร้าน B จะมีสมการเป็น 6.50r + 8.00b = 66.00

เมื่อทำการแก้ระบบสมการโดยการกำจัดก็จะได้ค่า r และค่า b ที่ทำให้ระบบสมการเป็นจริงด้วยการคูณทั้งสองข้างของสมการร้าน A ด้วย 6.5 จะได้ (5.50r)(6.5) + (3.00b)(6.5) = (37.00)(6.5) หรือ 35.75r + 19.5b = 240.5

จากนั้นทำการคูณทั้งสองด้านของสมการร้าน B ด้วย 5.5 จะได้ (6.50r)(5.5) + (8.00b)(5.5) = (66.00)(5.5) หรือ 35.75r + 44b = 363 และเมื่อลบทั้งสองด้านของสมการร้าน A 35.75r + 19.5b = 240.5 จากด้านที่สอดคล้องกันของสมการร้าน B 35.75r + 44b = 363

จะได้ (35.75r − 35.75r) + (44b − 19.5b) = (363 − 240.5) หรือ 24.5b = 122.5 จากนั้นทำการหารทั้งสองด้านของสมการนี้ด้วย 24.5 ก็จะได้ b = 5

ดังนั้นจึงสรุปได้ว่าซื้อแบล็กเบอร์รี่ไปทั้งหมดจำนวน 5 ไพนต์

• อสมการเชิงเส้น 1-2 ตัวแปร (Linear Inequalities in 1 or 2 Variables)

ตัวอย่างข้อสอบ

Figure A and figure B are both regular polygons. The sum of the perimeter of figure A and the perimeter of figure B is 63 inches. The equation 3x + 6y = 63 represents this situation, where x is the number of sides of figure A and y is the number of sides of figure B.

Which statement is the best interpretation of 6 in this context?

A) Each side of figure B has a length of 6 inches.

B) The number of sides of figure B is 6.

C) Each side of figure A has a length of 6 inches.

D) The number of sides of figure A is 6.

ข้อนี้ตอบ A เพราะจากคำอธิบายระบุว่ารูป A และรูป B (ไม่มีรูปประกอบ) เป็นรูปหลายเหลี่ยมปกติทั้งคู่ และผลรวมของเส้นรอบวงของรูปทั้งสองมีค่าเท่ากับ 63 นิ้ว

นอกจากนี้ยังกำหนดว่า x คือจำนวนด้านของรูป A และ y คือจำนวนด้านของรูป B เมื่อลองแทนสมการว่า “3x + 6y = 63” ก็จะได้ค่าเท่ากับ 63 ตามที่โจทย์ระบุเอาไว้

ดังนั้น 3x และ 6y จึงแสดงถึงเส้นรอบรูปของ A และรูป B ตามลำดับ (หน่วยเป็นนิ้ว) และ y คือจำนวนด้านของรูป B ดังนั้น จึงสรุปได้ว่าแต่ละด้านของรูป B มีความยาว 6 นิ้ว

2. Advanced Math (คณิตศาสตร์ขั้นสูง)

ข้อสอบในหัวข้อ Advanced Math หรือข้อสอบคณิตศาสตร์ขั้นสูง จะมีจำนวนทั้งหมด 13 – 15 ข้อ คิดเป็น 35% ของข้อสอบ โจทย์จะเน้นไปที่การวัดทักษะด้านการแก้สมการคณิตศาสตร์เชิงลึกที่สามารถนำเอาไปต่อยอดและประยุกต์ใช้ในการเรียนสาย STEM (Science, Technology, Engineer, Math) แบ่งหัวข้อการสอบย่อยได้ 4 เรื่อง ดังนี้

• นิพจน์เทียบเท่า (Equivalent Expressions)

ตัวอย่างข้อสอบ

ข้อนี้ตอบ A เพราะการลบนิพจน์ตรรกยะหนึ่งจากอีกนิพจน์หนึ่ง ตัวส่วนของนิพจน์จะต้องเท่ากัน เนื่องจาก 4x – 5 และ x + 1 ไม่มีตัวประกอบร่วมกัน นิพจน์ตรรกยะแต่ละนิพจน์จึงควรเขียนและแจกแจงใหม่ ดังนี้

• อสมการไม่เชิงเส้น 1 ตัวแปร (Nonlinear Equations in 1 variable)

ตัวอย่างข้อสอบ

(x − 1)² = −4

How many distinct real solutions does the given equation have?

A) Exactly one

B) Exactly two

C) Infinitely many

D) Zero

ข้อนี้ตอบ D เพราะค่าใดก็ตามที่มีค่าเป็นบวกหรือลบก็จะมีค่าเป็นบวกเมื่อยกกำลังสอง ดังนั้นด้านซ้ายมือของสมการที่กำหนดจะเป็นบวกหรือศูนย์สำหรับค่า x ใด ๆ ก็ตาม เนื่องจากด้านขวามือของสมการที่กำหนดเป็นลบ จึงไม่มีค่า x ใดเลยที่สมการที่กำหนดเป็นจริง

ดังนั้นจำนวนคำตอบจริงที่แตกต่างกันสำหรับสมการที่กำหนดจึงเป็นศูนย์

• ระบบสมการสองตัวแปร (Systems of Equations in 2 Variables)

ตัวอย่างข้อสอบ

In the xy-plane, a line with equation 2y = 4.5 intersects a parabola at exactly one point. If the parabola has equation y = −4×2 + bx, where b is a positive constant, what is the value of b?

ข้อนี้ตอบ 6 เพราะเมื่อกำหนดให้เส้นตรงที่มีสมการ 2y = 4.5 ตัดกับพาราโบลาที่มีสมการ y = −4×2 + bx

โดยที่ b เป็นค่าคงที่บวก ณ จุดเดียวบนระนาบ xy ระบบสมการที่ประกอบด้วย 2y = 4.5 และ y = −4×2 + bx จึงมีคำตอบเพียงคำตอบเดียว

เมื่อหารทั้งสองข้างของสมการของเส้นตรงด้วย 2 จะได้ผลลัพธ์ y = 2.25 เมื่อแทนค่า y ด้วย 2.25 ในสมการของพาราโบลา จะได้ผลลัพธ์ 2.25 = −4×2 + bx การบวก 4×2 และลบ bx ออกจากทั้งสองด้านของสมการนี้ให้ผลลัพธ์ 4×2 – bx + 2.25 = 0

สมการกำลังสองในรูปของ ax2 + bx + c = 0 โดยที่ a, b และ c เป็นค่าคงที่ มีคำตอบเดียวเมื่อตัวแยก b2 − 4ac มีค่าเท่ากับศูนย์ การแทนค่า a ด้วย 4 และ 2.25 ด้วย c ในนิพจน์ b2 − 4ac และตั้งค่านิพจน์นี้ให้เท่ากับ 0 จะได้ b2 − 4(4)(2.25) = 0 หรือ b2 − 36 = 0 การบวก 36 ในแต่ละด้านของสมการนี้จะได้ b2 = 36

เมื่อนำรากที่สองของแต่ละด้านของสมการนี้มาหารด้วย b = ±6 สมการนี้กำหนดให้ b เป็นค่าบวก

ดังนั้น b จึงมีค่าเท่ากับ 6

• ฟังก์ชันไม่เชิงเส้น (Nonlinear Functions)

ตัวอย่างข้อสอบ

g(x) = x² + 55

What is the minimum value of the given function?

A) 3,025

B) 110

C) 55

D) 0

ข้อนี้ตอบ C เพราะเมื่อถอดฟังก์ชันกำลังสองในรูปแบบ g(x) = a(x − ℎ)² + k โดยที่ a, h และ k เป็นค่าคงที่ มีค่าต่ำสุดของ k ที่ x = ℎ เมื่อ a > 0 จะสามารถเขียนใหม่เป็น g(x) = 1(x − 0)²  + 55 โดยที่ ℎ = 0 และ k = 55

ดังนั้นค่าต่ำสุดของฟังก์ชันที่กำหนดคือ 55

3. Problem Solving and Data Analysis (การแก้ไขโจทย์ปัญหาและวิเคราะห์ข้อมูล)

ข้อสอบในหัวข้อ Problem Solving and Data Analysis จะเน้นโจทย์ปัญหาคณิตศาสตร์ที่วัดทักษะด้านการใช้เหตุผลในการแก้ไขปัญหาและวิเคราะห์ข้อมูลเชิงปริมาณ การคำนวณอัตราส่วน, ร้อยละ, ความน่าจะเป็น รวมไปถึงการวิเคราะห์และตีความข้อมูลแบบตัวแปรเดียวและสองตัวแปรที่มักพบได้ในชีวิตประจำวัน  มีจำนวนทั้งหมด 5 – 7 ข้อ คิดเป็น 15% ของข้อสอบทั้งหมด ประกอบไปด้วย 7 เรื่องย่อย ได้แก่

• อัตราส่วน, ความสัมพันธ์ตามสัดส่วนและหน่วย (Ratios, rates, proportional relationships, and units)

ตัวอย่างข้อสอบ

The density of a certain type of wood is 353 kilograms per cubic meter. A sample of this type of wood is in the shape of a cube and has a mass of 345 kilograms. To the nearest hundredth of a meter, what is the length of one edge of this sample?

A) 0.98

B) 0.99

C) 1.01

D) 1.02

ข้อนี้ตอบ B เพราะโจทย์กำหนดให้ความหนาแน่นของไม้อยู่ที่ 353 กิโลกรัมต่อลูกบาศก์เมตร (kg/m³) โดยไม้มีมวล 345 กิโลกรัม

เนื่องจากตัวอย่างไม้ประเภทนี้มีลักษณะเป็นลูกบาศก์ จึงสามารถหาความยาวของขอบด้านหนึ่งของตัวอย่างได้โดย

ใช้สูตรปริมาตรของลูกบาศก์ V = s³ โดยที่ V แทนปริมาตรเป็น m³ และ s แทนความยาวเป็น m ของขอบด้านหนึ่งของลูกบาศก์

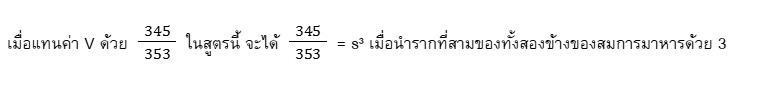
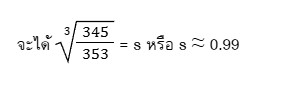
ดังนั้นความยาวของขอบด้านหนึ่งของตัวอย่างไม้ที่ใกล้เคียงที่สุดจึงเท่ากับ 0.99

• ร้อยละ (Percentages)

ตัวอย่างข้อสอบ

In a group, 40% of the items are red. Of all the red items in the group, 30% also have stripes. What percentage of the items in the group are red and have stripes?

A) 10%

B) 12%

C) 70%

D) 75%

ข้อนี้ตอบ B เพราะโจทย์กำหนดให้ 40% ของกลุ่มเป็นสีแดง จึงสามารถเขียนเป็น 0.4x โดย x แทนจำนวนรายการทั้งหมดในกลุ่ม และของสีแดงอีก 30% มีแถบ

ดังนั้นจำนวนรายการในกลุ่มที่เป็นสีแดงและมีแถบสามารถแสดงด้วย 0.3(0.4x) หรือ 0.12x นิพจน์ 0.12x แทน 12% ของ x และเนื่องจาก x แทนจำนวนรายการทั้งหมดในกลุ่ม จึงสรุปได้ว่าสิ่งของสีแดงที่มีแถบมีจำนวนทั้งหมด 12%

• ข้อมูลตัวแปรเดียว: การกระจายและการวัดจุดศูนย์กลาง (One-variable data: distributions and measures of center and spread)

ตัวอย่างคำถาม

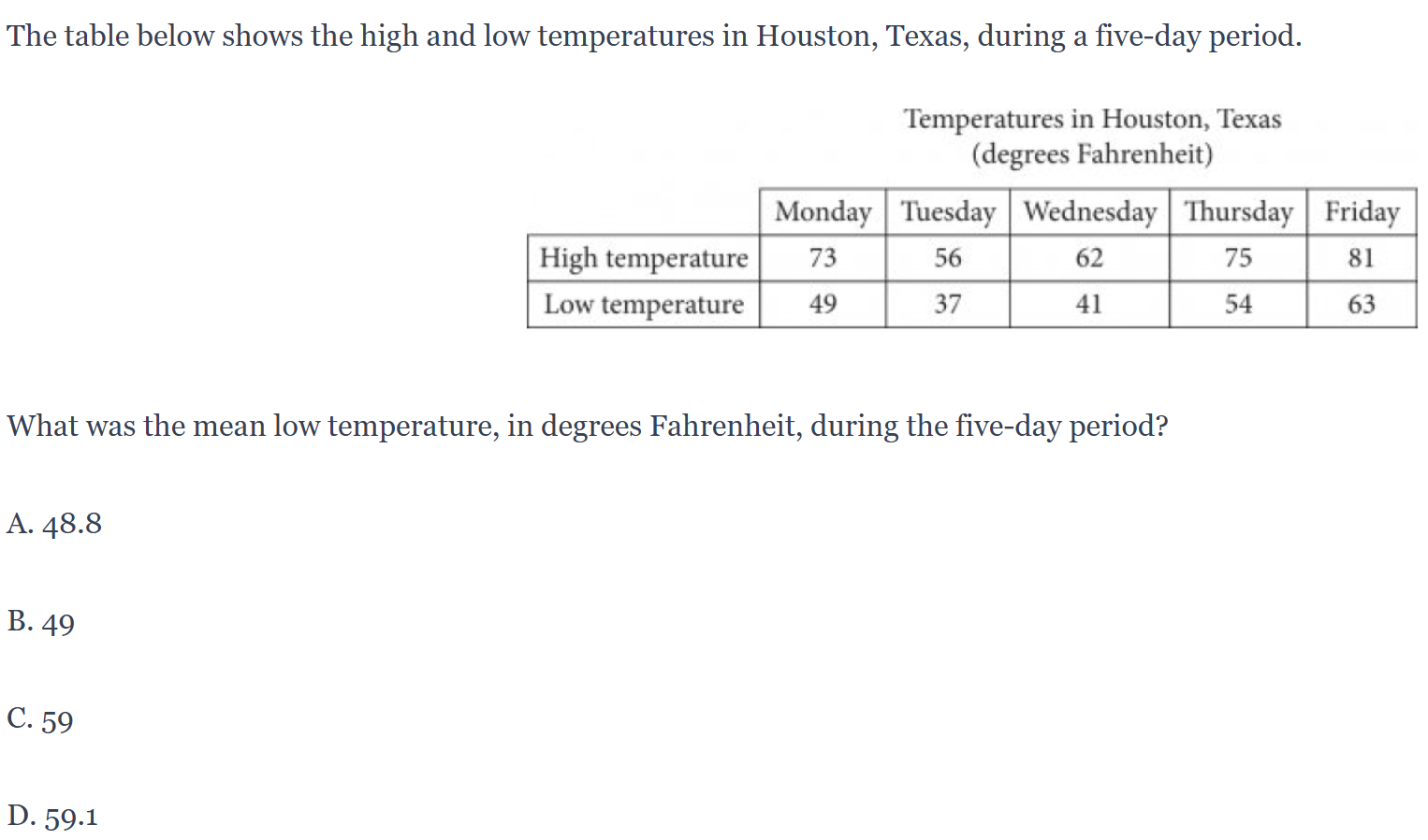
ข้อนี้ตอบ A เพราะเมื่อนำเอาค่าของอุณหภูมิต่ำสุดของแต่ละวันมาหาผลรวม (บวก) จะได้เท่ากับ 49+37+41+54+63 = 244 และเมื่อนำไปหาค่าเฉลี่ยโดยหารจำนวนวันทั้งหมด (5 วัน) ก็จะได้ 244/5 = 48.8 ซึ่งก็แปลว่าอุณหภูมิเฉลี่ยต่ำสุดเท่ากับ 48.8 นั่นเอง

• ข้อมูลสองตัวแปร: โมเดลและกราฟแบบกระจาย (Two-variable data: models and scatter plots)

ตัวอย่างคำถาม

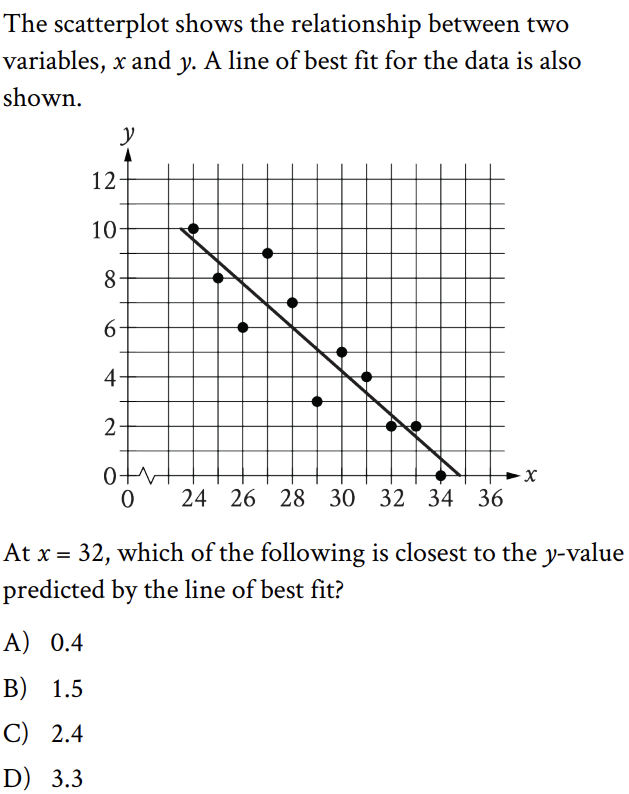
ข้อนี้ตอบ C เพราะ เมื่อ x = 32 ก็ทำให้เส้นที่เหมาะสมของค่า y อยู่ที่ระหว่าง 2 และ 3 ซึ่งค่าที่ใกล้เคียงที่สุดก็คือ 2.4 นั่นเอง

• ความน่าจะเป็นและหลักความน่าจะเป็นแบบมีเงื่อนไข (Probability and conditional probability)

ตัวอย่างข้อสอบ

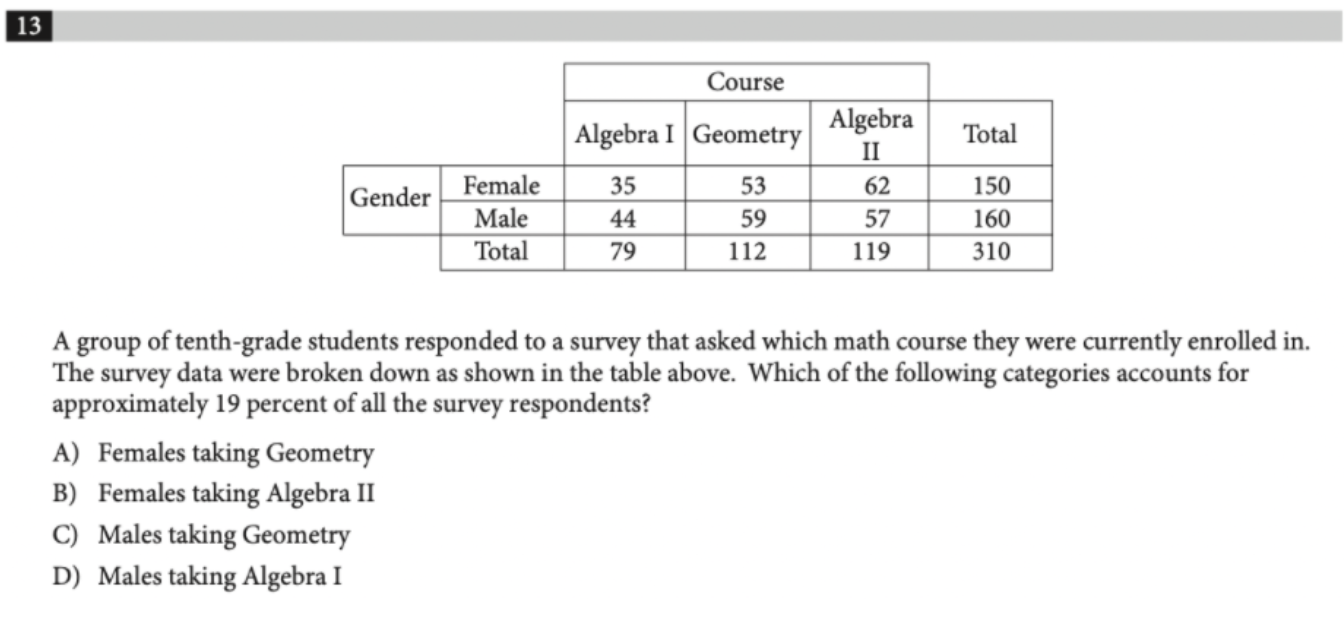
ข้อนี้ตอบ C เพราะโจทย์ระบุว่า 19% ของผู้ตอบแบบสำรวจทั้งหมด ซึ่งเมื่อดูจากตารางแล้วก็จะพบว่ามีจำนวนผู้ตอบแบบสอบถามทั้งหมด 310 คน และสามารถเขียนสมการได้

โดยเมื่อถอดสมการออกมาแล้วก็จะเท่ากับ 58.9 ซึ่งก็ใกล้เคียงกับ 59 มากที่สุด จึงตีความได้ว่า 19% ของจำนวนประชากรทั้งหมดคือนักเรียนชายที่ลงเรียนวิชาเรขาคณิต

• การอนุมานจากสถิติตัวอย่างและขอบเขตของข้อผิดพลาด (Inference from sample statistics and margin of error)

ตัวอย่างข้อสอบ

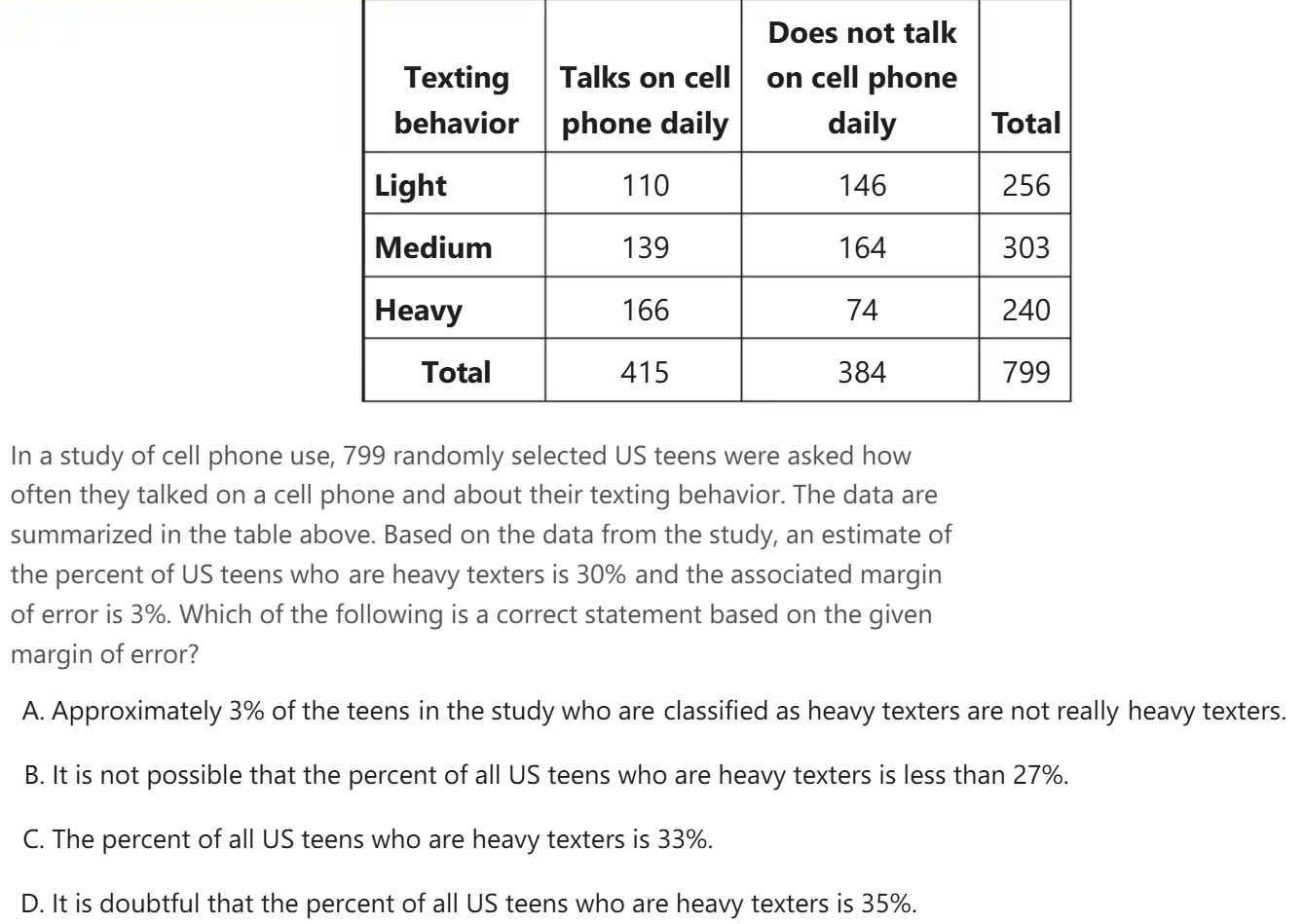
ข้อนี้ตอบ D เพราะโจทย์กำหนดค่าความคลาดเคลื่อนไว้ที่ 3% ดังนั้นจำนวนเปอร์เซ็นต์ที่วัยรุ่นอเมริกันน่าจะส่งข้อความมากเกินควรก็จะอยู่ภายใน 3% ของค่าประมาณ 30% หรือระหว่าง 27% – 33% ดังนั้นข้อ D ที่มีจำนวนเปอร์เซ็นต์เกินมาจากข้อมูลข้างต้นจึงเป็นข้อที่ถูกต้องนั่นเอง

• การประเมินสถิติผ่านการสังเกตและทดลอง (Evaluating statistical claims: observational studies and experiments)

ตัวอย่างคำถาม

To determine the mean number of children per household in a community, Tabitha surveyed 20 families at a playground. For the 20 families surveyed, the mean number of children per household was 2.4. Which of the following statements must be true?

A) The mean number of children per household in the community is 2.4.

B) A determination about the mean number of children per household in the community should not be made because the sample size is too small.

C) The sampling method is flawed and may produce a biased estimate of the mean number of children per household in the community.

D) The sampling method is not flawed and is likely to produce an unbiased estimate of the mean number of children per household in the community.

ข้อนี้ตอบ C เพราะการสุ่มกลุ่มตัวอย่างจากครอบครัวที่พบในสนามเด็กเล่นเป็นวิธีการที่ไม่เที่ยงตรง อาจทำให้เกิดความคลาดเคลื่อนของจำนวนกลุ่มตัวอย่างซึ่งส่งผลต่อการทดลองได้ เพราะหลาย ๆ ครอบครัวอาจไม่ได้พาลูกมาที่สนามเด็กเล่นในวันนั้น ๆ หรือบางครอบครัวอาจไม่ได้อาศัยอยู่ในชุมชนดังกล่าวแต่บังเอิญพาลูกมาเล่นที่สนามเด็กเล่นในวันที่ลงไปเก็บข้อมูล หากต้องการเก็บข้อมูลก็ควรที่จะหาข้อมูลอย่างละเอียดก่อนทำการสุ่มกลุ่มตัวอย่าง

4. Geometry and Trigonometry (เรขาคณิตและตรีโกณมิติ)

ข้อสอบในหัวข้อ Geometry and Trigonometry หรือโจทย์เรขาคณิตและตรีโกณมิติ จะมีทั้งหมด 5 – 7 ข้อ คิดเป็น 15% ของข้อสอบทั้งหมด โจทย์จะเน้นการวัดความสามารถในการแก้โจทย์เรขาคณิตทั้งสองมิติและสามมิติ รวมถึงการแก้โจทย์ด้านตรีโกณมิติ แบ่งหัวข้อการสอบย่อยได้ 4 เรื่อง ดังนี้

• การหาพื้นที่และปริมาตร (Area and volume formulas)

ตัวอย่างคำถาม

On average, one square inch of human skin contains 650 sweat glands. A certain area of skin contains 1,170 sweat glands. Based on this information, which of the following is closest to the size of this area, in square inches?

A) 0.44

B) 0.56

C) 0.80

D) 1.80

ข้อนี้ตอบ D เพราะเมื่อนำเอาจำนวนต่อมเหงื่อต่อตารางนิ้วมาหารกับจำนวนต่อมเหงื่อทั้งหมดก็จะได้พื้นที่หน่วยตารางนิ้ว (1170/650 = 1.8)

• เส้นตรง, มุม และสามเหลี่ยม (Lines, angles, and triangles)

ตัวอย่างคำถาม

Two nearby trees are perpendicular to the ground, which is flat. One of these trees is 10 feet tall and has a shadow that is 5 feet long. At the same time, the shadow of the other tree is 2 feet long. How tall, in feet, is the other tree?

A) 3

B) 4

C) 8

D) 27

ข้อนี้ตอบ B เพราะสามารถจำลองต้นไม้และเงาได้โดยใช้รูปสามเหลี่ยมมุมฉาก ซึ่งความสูงของต้นไม้และความยาวของเงาจะเท่ากับด้านของสามเหลี่ยม

ดังนั้นหากกำหนดความสูงของต้นไม้อีกต้นหนึ่งเป็น x ฟุต ก็จะสามารถเขียนสมการได้ ดังนี้

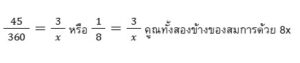
เมื่อคูณด้านของสมการออกมาก็จะได้คำตอบว่า x = 4 จึงสรุปได้ว่าต้นไม้อีกต้นหนึ่งสูง 4 ฟุต

• สามเหลี่ยมมุมฉากและตรีโกณมิติ Right triangles and trigonometry

ตัวอย่างคำถาม

The length of a rectangle’s diagonal is 5 √17, and the length of the rectangle’s shorter side is 5. What is the length of the rectangle’s longer side?

1. A)  √17 17
2. B) 20
3. C)  15√2
4. D) 400

ข้อนี้ตอบ B เพราะเมื่อลากเส้นทแยงมุมบนรูปสี่เหลี่ยมผืนผ้าจะได้เป็นสามเหลี่ยมมุมฉากขนาดเท่ากัน โดยมีเส้นทแยงมุมเป็นด้านตรงข้ามมุมฉากของสามเหลี่ยมทั้งสองรูป ความยาวของเส้นทแยงมุมคือ 5 √17

โดยมีความกว้างของสี่เหลี่ยมผืนผ้าที่ 5 และสามารถหาความยาวได้ด้วยใช้ทฤษฏีบทพีทาโกรัส a² + b²= c² โดยที่ a และ b คือความยาวของด้านตรงข้ามมุมฉาก ส่วน c คือความยาวของด้านตรงข้ามมุมฉากของรูปสามเหลี่ยม

จากนั้นนำเอาตัวเลขใส่สมการจะได้เป็น 5² + b²=  ถอดสมการได้เป็น 25 + b²= (5√17)² หรือ 25 + b²= 425 และเมื่อลบ 25 ทั้งสองข้างของสมการก็จะได้คำตอบว่า b²= 400 ซึ่งรากที่ 2 ของ 400 คือ 20 ดังนั้นจึงสรุปได้ว่าสี่เหลี่ยมผืนผ้ายาว 20 นั่นเอง

• วงกลม (Circles) จุดศูนย์กลาง, รัศมี

ตัวอย่างคำถาม

A circle has center O, and points A and B lie on the circle. The measure of arc AB is 45° and the length of arc AB is 3 inches. What is the circumference, in inches, of the circle?

A) 3

B) 6

C) 9

D) 24

ข้อนี้ตอบ D เพราะเมื่อกำหนดให้ส่วนของ AB มีขนาด 45° และมีความยาว 3 นิ้ว ซึ่งเส้นรอบวงทั้งหมดมีขนาด 360° หาก x แทนเส้นรอบวงเป็นนิ้วของวงกลม จะได้สมการดังนี้

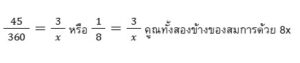
จะได้ 1(x) = 3(8) หรือ x = 24

เทคนิคพิชิตข้อสอบ SAT Math

เป็นยังไงกันบ้างกับแนวข้อสอบ SAT Math ที่พี่กริฟฟินยกตัวอย่างมาให้น้อง ๆ ลองทำกันดู จะเห็นได้ว่าข้อสอบแต่ละข้อมีความซับซ้อนต่างกันออกไปตามการคละกันของความยากง่ายของข้อสอบที่สามารถพบได้จริง ซึ่งถ้าน้องคนไหนเรียนสายวิทย์-คณิตมาก็น่าจะสอบผ่านได้ไม่ยาก ส่วนใครที่เรียนสายศิลป์แล้วจำเป็นต้องใช้คะแนนความถนัดทางคณิตศาสตร์เพื่อเรียนต่อคณะในฝันก็ไม่ต้องกังวลไป เพราะพี่กริฟฟินสรุปทริกเตรียมสอบดี ๆ มาฝากกันด้วยดังนี้

1. เตรียมท่องศัพท์ทางคณิตศาสตร์
2. อ่านสอบทีละเรื่อง ฝึกทำโจทย์ตามหัวข้อที่ออกสอบ
3. ฝึกใช้งานแอปพลิเคชัน Bluebook และทำความคุ้นเคยกับเครื่องคิดเลข

คำถามที่พบบ่อยเกี่ยวกับการสอบ SAT Math

สมัครสอบ SAT Math ยังไง? ค่าสอบเท่าไร

ถ้าใครต้องการลงสมัครสอบ SAT Math จะต้องทำการลงสอบพร้อมกับ SAT Verbal ควบคู่กันไป โดยอัตราค่าสมัครสอบจะอยู่ที่ครั้งละ 111 USD (ค่าสมัครสอบ 68 USD และค่าธรรมเนียมการสอบนอกสหรัฐอเมริกา 43 USD) ส่วนวิธีการสมัครสอบก็สามารถเข้าไปดู 9 ขั้นตอนสมัครสอบ SAT ด้วยตนเอง และเปิดเว็บไซต์สมัครสอบไปพร้อมกับพี่กริฟฟินได้เลย

ควรได้คะแนน SAT Math ขั้นต่ำที่เท่าไร?

มหาวิทยาลัยแต่ละแห่งก็จะมีการกำหนดเกณฑ์ขั้นต่ำของคะแนนที่แตกต่างกันออกไปตามคณะที่น้อง ๆ สนใจเข้าเรียน แต่ในเบื้องต้นขอแนะนำให้ทำคะแนนขั้นต่ำที่ 400 คะแนน (ครึ่งหนึ่งของคะแนนเต็ม) ก็สามารถยื่นเข้าคณะอินเตอร์ดัง ๆ ได้แล้ว แต่ยิ่งทำคะแนนได้สูง โอกาสที่จะสอบติดก็มีมากกว่า จึงแนะนำให้เตรียมตัวอ่านสอบและทำโจทย์เยอะ ๆ เพื่อเพิ่มโอกาสในการยื่นเข้าเรียนในมหาวิทยาลัยที่หลากหลายมากยิ่งขึ้น (สามารถตรวจสอบเกณฑ์คะแนน SAT ขั้นต่ำสำหรับการยื่นเรียนต่อคณะอินเตอร์ได้ ที่นี่)

ศูนย์สอบ SAT 2025 มีที่ไหนบ้าง

โรงเรียนนานาชาติส่วนหนึ่งในประเทศไทยได้ขึ้นทะเบียนเป็นศูนย์สอบ SAT อย่างเป็นทางการ จึงทำให้มีตัวเลือกศูนย์สอบกว่า 50 แห่งทั่วประเทศ แต่ศูนย์สอบส่วนมากจะมีการเปิดรอบสอบที่ต่างกัน จึงแนะนำให้ทำการเช็ครอบสอบที่ต้องการใน เว็บไซต์ โดยเลือก “ประเทศไทย” และเลือกวันสอบที่ต้องการ ก็จะมีรายชื่อศูนย์สอบที่เปิดสอบในรอบที่ต้องการปรากฏขึ้นมา โดยศูนย์สอบ SAT ในกรุงเทพ มีทั้งหมด 25 แห่ง

ลงติวเพิ่มความมั่นใจ เสริมจุดแข็งและปิดจุดอ่อน

สุดท้ายนี้ ถ้าน้องคนไหนมีเวลาฝึกทำสอบจำกัด หรือเรียนในสายศิลป์มาและอยากเสริมความมั่นใจก่อนสอบ SAT Math ขอแนะนำให้ลง ติวสอบ SAT กับ House of Griffin อุ่นใจกว่า เลือกติวได้ทั้งคอร์ส SAT ขั้นเริ่มต้นตั้งแต่ปูพื้นฐาน, คอร์สตะลุยโจทย์, คอร์สปิดจุดอ่อน, คอร์สติวแบบเร่งด่วน รวมไปถึงคอร์สติวเข้มแบบจัดเต็มพร้อมการันตีคะแนนสอบก็มีให้เลือกลงเรียนตามความต้องการของน้อง ๆ ทุกคน