สรุปพีชคณิตข้อสอบ SAT Math ควรเน้นตรงไหน มีหลักการทำอย่างไรบ้าง

น้องคนไหนกำลังเตรียมตัวไปสอบ SAT แล้วมีความกังวลกับการสอบ SAT Math ที่เป็นข้อสอบวัดความถนัดทางคณิตศาสตร์และความสามารถในการคิดคำนวณอยู่ โดยเฉพาะข้อสอบในพาร์ท “พีชคณิต” หรือ Heart of Algebra ที่มีจำนวน 13 – 15 ข้อ หรือคิดเป็นประมาณ 35% ของข้อสอบทั้งหมด จึงเป็นส่วนที่ควรทบทวนให้แม่นยำและไม่ควรมองข้ามเลย ดังนั้นหากมีความรู้ความเข้าใจเกี่ยวกับโจทย์ในหัวข้อนี้มากพอก็จะช่วยเพิ่มคะแนนของ SAT Math ได้เป็นอย่างดี

วันนี้พี่กริฟฟินเลยจะพาทุกคนมาศึกษาเกี่ยวกับหลักการทำข้อสอบพีชคณิตกันแบบเจาะลึก โดยแบ่งหัวข้อการสอบออกเป็น 5 หัวข้อย่อย ได้แก่ หลักการทำสมการเชิงเส้น 1 ตัวแปร, 2 ตัวแปร, หลักการทำระบบสมการเชิงเส้นสองตัวแปร, หลักการทำฟังก์ชันเชิงเส้น และหลักการทำอสมการเชิงเส้นหนึ่งและสองตัวแปร

ซึ่งมีข้อมูลค่อนข้างเยอะ จึงจะขอแบ่งบทความเรื่องนี้จะแบ่งออกเป็น 2 Part และสำหรับใน Part 1 ก็จะแนะนำเกี่ยวกับการทำความรู้จักกับพีชคณิตขั้นเบื้องต้น และการทำโจทย์ในหัวข้อสมการเชิงเส้นแบบ 1 และ 2 ตัวแปร รวมทั้งระบบสมการเชิงเส้นสองตัวแปรกันก่อน

พีชคณิต คืออะไร

Algebra หรือพีชคณิต เป็นศาสตร์หนึ่งในรายวิชาคณิตศาสตร์ที่มีการนำเอาตัวอักษร เช่น  x, y หรือสัญลักษณ์ต่าง ๆ มาสมมติตัวแปรไม่ทราบค่า แทนที่จะใช้เพียงแค่ตัวเลขเพียงอย่างเดียว เพื่อประกอบให้เห็นถึงโครงสร้างของสมการและอสมการ รวมไปถึงความสัมพันธ์ภายในตัวโจทย์ปัญหาได้ชัดเจนยิ่งขึ้น และนำไปสู่การแก้ไขโจทย์คณิตศาสตร์ได้ง่ายขึ้น ซึ่งข้อสอบ SAT Math ที่เน้นวัดความสามารถในการวิเคราะห์และแก้ไขปัญหาโจทย์คณิตศาสตร์ก็มีโจทย์ปัญหาในหัวข้อนี้ด้วยเช่นกัน

หลักการทำสมการเชิงเส้น 1 ตัวแปร (Linear equation with 1 variable)

สมการเชิงเส้น 1 ตัวแปร หรือสมการเชิงเส้นตัวแปรเดียว หมายถึงโจทย์คณิตศาสตร์ที่มีการแทนค่าสมการเพียงแค่ 1 ค่าในข้อคำถามนั้น ๆ (ส่วนมากจะใช้ x แทนตัวแปรในสมการที่ยังไม่ทราบค่า) ซึ่งตัวสมการนั้นมีค่าชี้กำลังสูงสุดเป็น 1 เสมอ (x¹ หรือ x) สมการเชิงเส้นตัวแปรเดียว หรือสมการเชิงเส้น 1 ตัวแปร จะมีรูปแบบทั่วไป คือ ax+b= 0 โดยที่ a กับ b เป็นค่าคงที่ และ a ไม่เท่ากับ 0 โดยหากเป็นโจทย์ปัญหาในรูปแบบข้อความ จะมีข้อความไม่ทราบค่าที่มีความสัมพันธ์ทั้งทางตรงและทางอ้อมของสมการระบุอยู่ (อาจมีข้อความเดียวหรือหลายข้อความ ขึ้นอยู่กับความซับซ้อนของโจทย์)

ทั้งนี้ ตัวแปรที่ไม่ทราบค่า (x) จะสามารถอยู่ในตำแหน่งด้านหน้าหรือด้านหลังเครื่องหมายเท่ากับ (=) ก็ได้ และเมื่อแทนค่าตัวแปร (x) ออกมาแล้วสมการเป็นจริง ก็จะถือว่าเป็นค่าที่คำนวณออกมาได้เป็นคำตอบของสมการนั้นนั่นเอง

สมบัติของสมการเชิงเส้นตัวแปรเดียว

สมการเชิงเส้นตัวแปรเดียว จะใช้การโดยแทนค่า a, b, c, d เป็นจำนวนใด ๆ ซึ่งเป็นได้ทั้งเลขจำนวนเต็มที่มีค่าเป็นบวกหรือลบ หรือเศษส่วนก็ได้ แต่เมื่อแทนค่าลงไปแล้วผลลัพธ์ของสมการนั้นต้องเป็นจริง โดยส่วนใหญ่แล้วสมการเชิงเส้นแบบ 1 ตัวแปรจะมีคำตอบเพียงแค่คำตอบเดียวเท่านั้น สามารถจำแนกคุณสมบัติในการคำนวณหาค่าตัวแปรออกมาได้ 5 รูปแบบ ดังนี้

1. สมบัติสมมาตร

โจทย์ในรูปแบบนี้จะสามารถสลับค่าและสลับข้าง (ซ้าย-ขวา) ของสมการได้โดยที่สมการนั้น ๆ ยังคงเป็นจริงและมีผลลัพธ์ที่เท่ากัน (ถ้า a = b แล้ว b = a)

ตัวอย่างเช่น

3+5 = x โจทย์นี้ a = 3 และ b = 5 จะสามารถแก้สมการออกมาได้ว่า x = 8 ซึ่งเมื่อลองกลับค่าตัวเลขก็ยังคงได้ผลลัพธ์ที่เท่ากันอยู่ดังเดิม คือ 3+5 = 8 และ 5+3 = 8

2. สมบัติการถ่ายทอด

สมการในรูปแบบนี้จะสามารถแทนค่าจำนวนใด ๆ ที่โจทย์ระบุเอาไว้และแก้สมการออกมาให้เป็นจริงได้ (ถ้า a = b และ b = c แล้ว a = c)

ตัวอย่างเช่น

a+b = c หากสมการ 3+5 = x และ x = 4×2 เมื่อถอดสมการออกมาว่า x = 8 ซึ่งทำให้ผลลัพธ์ของสมการทั้งคู่เป็นจริง แสดงว่า 3+5 = 4×2 ซึ่งสมการที่มีคุณสมบัตินี้ก็จะเรียกว่า สมบัติถ่ายทอดของความเท่ากัน

3. สมบัติเท่ากันด้านการบวก

เมื่อสองจำนวนที่มีค่าเท่ากัน (อาจเป็นจำนวนบวกหรือจำนวนลบก็ได้) นำจำนวนอีกจำนวนหนึ่งมาบวกเข้ากับแต่ละจำนวนนั้น ๆ แล้ว ผลบวกของทั้งสองย่อมเท่ากัน (ถ้า a = b แล้ว a + c = b + c)

ตัวอย่างเช่น a+c = d และ b+c = d โดยกำหนดค่า a = 5×2 และ b = 10 ส่วน c เป็นจำนวนที่ยังไม่ทราบค่า (แทนด้วยสัญลักษณ์ x) และ d = 7 สามารถเขียนสมการออกมาได้ ดังนี้

(5×2)+x = 7 และ 10+x = 7 เมื่อแก้สมการออกมาแล้วได้ค่า x = -3 โดยที่สมการทั้งคู่เป็นจริง จึงสามารถสรุปได้ว่า a+c = b+c หรือในกรณีนี้ที่ค่า x ติดลบ ก็จะเขียนสมการได้ว่า a+(-c) = b+(-c) หรือ a-c = b-c จึงสรุปได้ว่าสมการข้างต้นนี้เป็นสมการที่มีสมบัติเท่ากันด้านการบวก

4. สมบัติเท่ากันด้านการคูณ

เมื่อจำนวนสองจำนวนที่มีเท่ากัน นำเอาจำนวนอีกจำนวนหนึ่งมาคูณเข้ากับจำนวนทั้งสองนั้น ผลลัพธ์ที่ออกมาย่อมมีค่าเท่ากัน (ถ้า a = b แล้ว ca = cb)

ตัวอย่างเช่น ac = bc โดยกำหนดค่า a = 8x แล้ว b = 16 และ c = 5 เมื่อเขียนสมการจะออกมาเป็น 8x(5) = 16(5) เมื่อแก้สมการจะได้คำตอบว่า x = 10 โดยที่สมการทั้งคู่เป็นจริง ดังนั้นแล้ว 8x(10) = 16(5) จึงเป็นสมการที่มีสมบัติเท่ากันด้านการคูณ เพราะทั้งคู่เป็นสมการที่เป็นจริงโดยมีคำตอบที่ 80 เหมือนกัน

5. สมบัติการแจกแจง

เมื่อจำนวนทั้งสองข้างของสมการ นำมาคูณเข้าไปในวงเล็บแล้ว ทำให้วงเล็บนั้นหายไป ผลลัพธ์ที่ได้ย่อมทำให้สมการเป็นจริงและมีค่าเท่ากัน a(b+c)= ab + ac

ตัวอย่างเช่น a(x+c) = ab+ac โดยกำหนดให้ a มีค่าเท่ากับ 2 และ c มีค่าเท่ากับ 3 ส่วน b เป็นจำนวนไม่ทราบค่า (แทนด้วยตัวแปร x) เมื่อเขียนสมการจะออกมาในรูป a(x+c) = ax+2(3) เมื่อถอดสมการออกมาแล้วจะได้ค่า b = 5 โดยที่สมการทั้งคู่เป็นจริง จึงสรุปได้ว่า 2(5+3) = 2(5) + 2(3) หรือ a(b+c) = ab+ bc

วิธีคิดคำตอบของสมการเชิงเส้นตัวแปรเดียว

สำหรับหลักการทำโจทย์ปัญหาเรื่องสมการเชิงเส้น 1 ตัวแปรในข้อสอบ SAT Math หากเป็นข้อที่เป็นโจทย์แบบเลือกตอบ (Multiple Choice) สามารถลองเอาตัวเลขในตัวเลือกคำตอบไปแทนค่าในสมการเพื่อเป็นทางลัดในการไขโจทย์ได้เลย ส่วนข้อคำถามที่เป็นข้อสอบแบบ Student Produced Response ที่ผู้สอบจะต้องเขียนคำตอบลงใน Answer Sheet ด้วยตัวเอง ก็จะต้องพิจารณาว่าโจทย์ถามอะไร แล้วใส่ตัวแปรแทนข้อความและนำตัวแปรไปสร้างความสัมพันธ์ในรูปแบบสมการ โดยการลองหาจำนวนมาแทนค่าในตัวสมการโดยการย้ายข้างสมการส่วนที่มีตัวแปรและค่าคงที่เอาไว้คนละข้างของเครื่องหมายเท่ากับ (หากเป็นสมการที่มีเศษส่วน ให้ทำส่วนของสมการให้เป็น 1 โดยการทำ ค.ร.น. (คูณร่วมน้อย) คูณทั้งสองข้างของสมการ) แล้วทำสัมประสิทธิ์ของตัวแปรให้เป็น 1 หรือสามารถใช้สมบัติของสมการในการช่วยหาคำตอบของสมการได้ เมื่อได้คำตอบออกมาแล้วให้สังเกตว่ามีความสอดคล้องกับโจทย์และทำให้สมการเป็นจริงหรือไม่ หากไม่สอดคล้องกันอาจเกิดจากการคิดเลขผิด หรือค่าสมการผิด ให้ลองตรวจคำตอบและคำนวณใหม่อีกครั้งหนึ่ง

ตัวอย่างข้อสอบ SAT Math ในหัวข้อสมการเชิงเส้นตัวแปรเดียว

สำหรับในหัวข้อของสมการเชิงเส้น 1 ตัวแปรหรือสมการเชิงเส้นตัวแปรเดียวนั้น เป็นหัวข้อที่มีจำนวนข้อสอบค่อนข้างน้อย เนื่องจากเป็นโจทย์ที่เรียกได้ว่าเป็นส่วนที่ “ง่ายที่สุด” จึงพบได้ไม่บ่อยนัก ใน 1 Module จะมีโจทย์ประเภทนี้เพียง 1-2 ข้อเท่านั้น ตัวอย่างเช่น

หลักการทำสมการเชิงเส้น 2 ตัวแปร (Linear equations in 2 variable)

สมการเชิงเส้น 2 ตัวแปร คือโจทย์คณิตศาสตร์ที่มีการแทนค่าสมการ 2 ตัวในข้อคำถามเพียง 1 ข้อ (ส่วนมากจะใช้ x หรือ y แทนตัวแปรในสมการที่ยังไม่ทราบค่า) และตัวสมการจะมีเลขชี้กำลังสูงสุดเป็น 1 เสมอ (x¹ หรือ x) มีรูปแบบสมการทั่วไปอยู่ที่ ax+by = c โดยที่ a, b และ c จะเป็นค่าคงที่ซึ่งเป็นได้ทั้งจำนวนเต็มที่มีค่าเป็นบวกหรือลบ หรือเศษส่วนก็ได้ ในขณะที่ x และ y เป็นตัวแปรไม่ทราบค่าที่จะสามารถอยู่ได้ทั้งด้านหน้าหรือด้านหลังเครื่องหมายเท่ากับ (=) ซึ่งเมื่อนำเอาไปพลอตกราฟจะได้เป็นเส้นตรง โจทย์ปัญหาในหัวข้อนี้จึงจะมีทั้งโจทย์ที่เป็นข้อความและโจทย์ที่เป็นกราฟนั่นเอง

เมื่อมีเรื่องกราฟก็ทำให้มีเรื่องของความชัน (m) เข้ามาเกี่ยวของด้วย ทำให้สามารถเขียนรูปแบบสมการใหม่ออกมาในรูป y = mx + c หรือ y = ax + b ได้ โดยที่ m แทนความชัน ส่วน b แทนจุดตัดของ y ซึ่งเมื่อเทียบกับรูปสมการทั่วไปของสมการเชิงเส้นสองตัวแปร (ax+by = c) ค่าความชันจะเท่ากับ -a/b

ข้อสังเกตของสมการเชิงเส้น 2 ตัวแปร

• มีตัวแปรสองตัว คือ x และ y หรืออาจใช้ตัวอักษรหรือสัญลักษณ์อื่น ขึ้นอยู่กับที่โจทย์ระบุ แต่จะมีจำนวนตัวแปรเพียงแค่ 2 ตัวเท่านั้น และจะมีสมการเพียงแค่ 1 สมการในโจทย์ 1 ข้อ
• ไม่มีการคูณกันของตัวแปร โดยอาจมีการคูณกันระหว่างตัวแปรกับค่าคงที่อื่น ๆ ภายในสมการ แต่จะไม่มีการคูณกันของตัวแปรในรูปแบบ xy ให้เห็น
• เลขชี้กำลังของตัวแปรเป็น 1 เสมอ
• สัมประสิทธิ์ของตัวแปรไม่เป็น 0 พร้อมกัน เมื่อ A = 0 สมการจะอยู่ในรูป By + C = 0
• ถ้าไม่ได้ระบุเงื่อนไขของ x และ y ให้กำหนดว่า x และ y เป็นจำนวนจริงเสมอ
• กราฟของสมการเชิงเส้น 2 ตัวแปรจะเป็นเส้นตรง จึงเรียกว่า “กราฟเส้นตรง” ซึ่งคำตอบของสมการเชิงเส้น 2 ตัวแปร ax+by = c คือจุดใดจุดหนึ่งในกราฟ โดยเมื่อพิกัด x คูณด้วย a และพิกัด y คูณด้วย b ผลรวมของค่าทั้งสองนี้จะเท่ากับ c
• สมบัติของสมการเชิงเส้น 2 ตัวแปรก็จะคล้ายคลึงกันกับสมบัติของสมการเชิงเส้น 1 ตัวแปร จึงสามารถนำเอามาปรับใช้งานเพื่อการแก้สมการได้เหมือนกัน
• ค่าความชัน จะมีอยู่ด้วยกัน 3 รูปแบบ ได้แก่ m > 0 กราฟของเส้นตรงจะทำมุมแหลมกับแกน x (ลาดขึ้น), m < 0 กราฟของเส้นตรงจะทำมุมป้านกับแกน x (ลาดลง) และถ้า m = 0 กราฟของเส้นตรงจะขนานกับแกน x (ไม่มีความชัน)

วิธีคิดคำตอบของสมการเชิงเส้น 2 ตัวแปร

ในส่วนของวิธีคิดคำตอบหรือการแก้สมการเชิงเส้น 2 ตัวแปรของข้อสอบ SAT Math น้อง ๆ จะต้องทำการพิจารณาและทำความเข้าใจเกี่ยวกับปัญหาที่โจทย์ต้องการถาม และมองหาเงื่อนไขและความสัมพันธ์ของข้อมูลต่าง ๆ ที่โจทย์ระบุมาให้อย่างละเอียดเพื่อที่จะสามารถวางแผนแก้ไขสมการออกมาให้ได้อย่างถูกต้อง โดยอาจใช้หลักการแก้สมการโดยการย้ายข้างสมการให้มีตัวแปรใดตัวแปรหนึ่งอยู่เพียงด้านเดียว หรือกำจัดตัวแปรตัวหนึ่งออกไปเพื่อหาค่าของตัวแปรอีกตัวหนึ่ง เมื่อได้คำตอบออกมาแล้วก็นำเอาคำตอบของตัวแปรที่ได้นั้นไปแทนค่าลงในสมการเริ่มต้นเพื่อหาค่าของตัวแปรที่เหลือ ซึ่งโดยปกติแล้ว สมการเชิงเส้นแบบ 2 ตัวแปรจะสามารถเขียนออกมาในรูปแบบกราฟและมองหาจุดตัดของกราฟเพื่อหาค่าสมการได้

ตัวอย่างเช่น

5x + 3y = 30

จะเห็นได้ว่าสมการข้างต้นมีตัวแปรสองตัว คือ x และ y และเมื่อนำมาขึ้นเป็นกราฟ จะสามารถแทนค่าตัวแปรใดตัวแปรหนึ่งเป็น 0 และทำการแก้สมการ จากนั้นนำเอาค่าของตัวแปรที่ได้มาแทนค่าและหาค่าของตัวแปรถัดไป ดังนี้

กำหนดให้ค่า y=0 จะสามารถเขียนสมการใหม่เพื่อหาค่าของ x ได้เป็น

5x + 3(0) = 30

โดยเมื่อจำนวนใด ๆ คูณเข้ากับเลข 0 จะทำให้จำนวนนั้นมีค่าเป็น 0 จากนั้นย้ายข้างสมการมาหารเพื่อหาค่า x ก็จะได้คำตอบว่า x = 6 นั่นเอง

จากนั้นหาค่าของ y เมื่อ x = 0 ก็จะเขียนสมการใหม่ได้ว่า

5 (0) + 3y = 30

และทำการย้ายข้างสมการไปหารเช่นเดียวกับวิธีข้างต้น ก็จะได้คำตอบว่า y = 10

โดยเมื่อนำเอามาพลอตกราฟจะอยู่ในรูปดังนี้

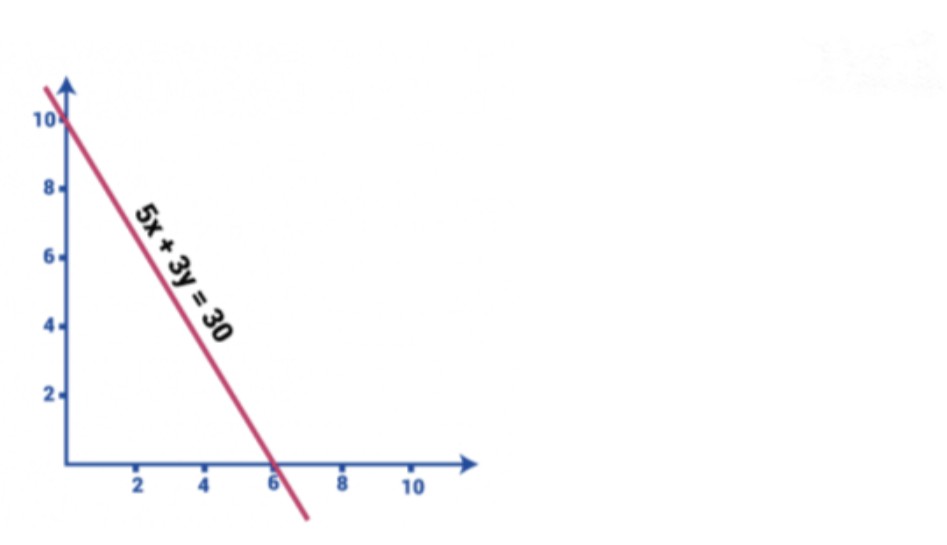
เมื่อเทียบค่าสมการแล้วก็จะได้คำตอบว่าจุดตัดแกน x หรือ a มีค่าเท่ากับ 2 และจุดตัดแกน y หรือ b มีค่าเท่ากับ 8

ทั้งนี้ สำหรับการทำข้อสอบที่เป็น Multiple Choice ยังสามารถนำเอาข้อที่เป็นตัวเลือกคำตอบของสมการที่เป็นคู่อันดับ (x, y) ไปแทนค่าในสมการก่อนเพื่อประหยัดเวลาการคำนวณ โดยหากแทนค่าแล้วผลออกมาว่าสมการเป็นจริงก็สามารถเลือกตอบข้อนั้นได้ทันที แต่สำหรับข้อที่เป็นการเขียนคำตอบก็สามารถใช้วิธีการแก้สมการด้านบนในการหาคำตอบได้เลย

ตัวอย่างข้อสอบ SAT Math ในหัวข้อสมการเชิงเส้น 2 ตัวแปร

ข้อคำถามในหัวข้อสมการเชิงเส้น 2 ตัวแปร จะเป็นคำถามที่พบได้ไม่บ่อยมากนัก แต่โดยเฉลี่ยแล้วจะมีจำนวนข้อมากกว่าสมการเชิงเส้นตัวแปรเดียว อาจมีคำถามในหัวข้อนี้ราว 2-3 ข้อใน 1 Module (ชุดข้อสอบ) ตัวอย่างคำถาม เช่น

1. The function g is defined by g(x) = 6x. For what value of x is g(x) = 54 ?

ข้อนี้ตอบ 9 เพราะเมื่อเขียนสมการออกเป็น g(x) = 6x เมื่อ g(x) = 54 ทำให้ค่า 6x = 54 และสามารถนำเอาตัวเลข 54 มาหาร 6 เพื่อหาค่า x ได้ ก็จะได้คำตอบออกมาว่า x = 9

2. Figure A and figure B are both regular polygons. The sum of the perimeter of figure A and the perimeter of figure B is 63 inches. The equation 3x + 6y = 63 represents this situation, where x is the number of sides of figure A and y is the number of sides of figure B.

Which statement is the best interpretation of 6 in this context?

1. A) Each side of figure B has a length of 6 inches.
2. B) The number of sides of figure B is 6.
3. C) Each side of figure A has a length of 6 inches.
4. D) The number of sides of figure A is 6.

ข้อนี้ตอบ A เพราะเนื่องจากรูป A และ B เป็นรูปหลายเหลี่ยม โดยผลรวมของเส้นรอบรูปคือ 63 นิ้ว นอกจากนี้ยังระบุว่า x คือจำนวนด้านของรูป A และ y คือจำนวนด้านของรูป B และโจทย์ระบุสมการมาว่าสมการ 3x + 6y = 63 แปลว่า 3x เส้นรอบรูป A และ 6y แทนเส้นรอบรูป B ซึ่งทั้งคู่มีหน่วยความยาวเป็นนิ้ว ดังนั้นจึงสรุปได้ว่าแต่ละด้านของรูป B มีความยาว 6 นิ้ว

ข้อนี้ตอบ B เพราะสามารถเขียนสมการออกมาในรูป y= a+bx y= bx+a โดยที่ b มีความชันของกราฟจำลองอยู่ที่ (0, a) ซึ่ง a คือจุดตัดของแทน y ซึ่งการกระจายของกราฟจะเห็นได้ว่าเมื่อค่า x เพิ่มขึ้นค่า y จะลดลง แปลว่ากราฟเชิงเส้นนี้มีความชันเป็นลบ ดังนั้น b<0 และจุดที่ใกล้กับค่าแกน y จะเป็นค่าบวกหรือ a>0 และจากตัวเลือกทั้งหมดก็มีเฉพาะแค่ข้อ B เท่านั้นที่ระบุว่าค่า y เป็นลบ ในขณะที่ค่า a ซึ่งเป็นพิกัดของจุดตัดแกน y มีค่าเป็นบวก

Kaylani used fabric measuring 5 yards in length to make each suit for a men’s choir. The relationship between the number of suits that Kaylani made, x, and the total length of fabric that she purchased y, in yards, is represented by the equation y − 5x = 6.

What is the best interpretation of 6 in this context?

1. A) Kaylani made 6 suits.
2. B) Kaylani purchased a total of 6 yards of fabric.
3. C) Kaylani used a total of 6 yards of fabric to make the suits.
4. D) Kaylani purchased 6 yards more fabric than she used to make the suits.

ข้อนี้ตอบ D เพราะสามารถเขียนสมการออกมาได้ว่า y-5x = 6 โดยที่ x ที่จำนวนชุด และ y แทนความยาวผ้า เมื่อบวก 5x เข้ากับสมการทั้ง 2 ข้างก็จะได้ y = 5x+6 เมื่อ y แทนจำนวนผ้าที่ซื้อ จึงสรุปออกมาได้ว่า Kaylani ซื้อผ้าจำนวน 5x หลา เพื่อทำชุดสูท และได้ซื้อผ้าเพิ่มอีก 6 หลาที่มากกว่าจำนวนผ้าที่ใช้ทำชุดสูททั้งหมด

ระบบสมการเชิงเส้น 2 ตัวแปร (Systems of 2 linear equations in 2 variables)

ระบบสมการเชิงเส้นสองตัวแปร คือ ชุดสมการเชิงเส้นสองตัวแปรที่มีการพิจารณาคำตอบร่วมกัน ในจุดนี้เมื่อดูจากชื่อแล้วอาจทำให้น้อง ๆ หลายคนอาจสับสนระหว่าง “สมการเชิงเส้น 2 ตัวแปร (Linear equations in 2 variables)” และ “ระบบสมการเชิงเส้น 2 ตัวแปร (Systems of 2 linear equations in 2 variables)” แม้ว่าโดยหลักการแล้วจะมีความคล้ายคลึงกันในบางส่วน แต่ระบบสมการเชิงเส้น 2 ตัวแปรจะมีความซับซ้อนกว่า และมีจำนวนสมการมากกว่า 1 สมการในข้อเดียว โดยที่คำตอบของสมการนั้น ๆ มีความเกี่ยวโยงกันอีกด้วย

โดยระบบสมการเชิงเส้น 2 ตัวแปร จะมีรูปแบบสมการเบื้องต้น ดังนี้

ax+by = e

cx+dy = f

โดยที่ a, b, c, d, e, f เป็นจำนวนจริง และ a, b กับ c, d ไม่เป็นศูนย์พร้อมกัน ซึ่งเราจะเรียกระบบสมการเชิงเส้น 2 ตัวแปรที่มี x และ y เป็นตัวแปร โดยที่ a และ c เป็นสัมประสิทธิ์ของ x ส่วน b และ d เป็นสัมประสิทธิ์ของ y

คำตอบของระบบสมการ 2 ตัวแปร

สำหรับคำตอบของระบบสมการเชิงเส้น 2 ตัวแปรจะสามารถแบ่งออกได้เป็น 3 ประเภทหลัก ๆ ตามรูปแบบของกราฟ ดังนี้

ระบบสมการที่มีคำตอบเพียงคำตอบเดียว จะมีจุดตัดกราฟอยู่ที่เพียงจุดเดียวเท่านั้น

ระบบสมการที่มีหลายคำตอบ (คำตอบเป็นอนันต์) กราฟของสมการจะทับกัน หรือตัดกันหลายจุด โดยที่สมการทั้งสองมีค่าสมประสิทธิ์เท่ากัน และมีค่าคงตัวเท่ากัน

ระบบสมการที่ไม่มีคำตอบ กราฟของสมการจะขนานกัน (กราฟไม่ตัดกัน) โดยที่สมการทั้งสองจะมีค่าสัมประสิทธิ์ที่เท่ากัน แต่มีค่าคงตัวต่างกัน

วิธีคิดคำตอบของระบบสมการเชิงเส้น

การหาคำตอบของระบบสมการเชิงเส้น จะสามารถแก้สมการได้ด้วย 3 วิธีหลัก ดังนี้

1. วิธีการหาจุดตัดกันของกราฟเพื่อแก้สมการ

วิธีนี้จะใช้การแทนค่าตัวแปรใดตัวแปรหนึ่งในสมการให้เป็น 0 ก่อน แล้วจึงนำมาหาค่าสมการ จากนั้นแทนค่าสมการอีกตัวหนึ่งโดยแทนตัวแปรที่เหลือในอีกสมการ (สมการที่ 2) เป็น 0 จากนั้นก็จะได้คำตอบของระบบสมการทั้ง 2 เส้น

ตัวอย่างเช่น

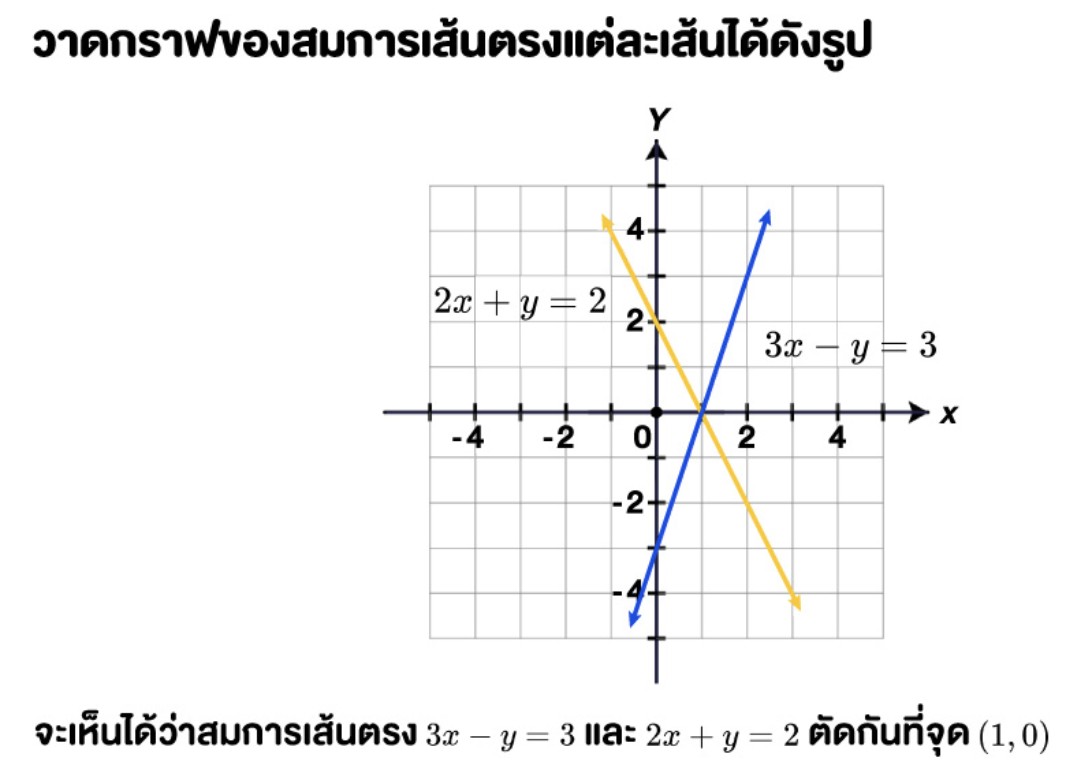
3x-y = 3 (สมการที่ 1)

2x+y =2 (สมการที่ 2)

หากใช้วิธีการหาจุดตัดกันของกราฟเพื่อแก้สมการ จะต้องทำการแทนค่าตัวแปรในสมการที่ 1 ดังนี้

3x-y = 3 เมื่อแทนค่า x เป็น 0 จะได้ค่า y = -3 หรือสรุปได้ว่าจุดตัดแกน y คือ (0,-3)

และเมื่อแทนค่า y เป็น 0 จะได้ค่า x = 1 หรือสรุปได้ว่าจุดตัดแกน x คือ (1,0)

จากนั้นแก้สมการที่ 2 โดยใช้วิธีเดียวกัน คือ แทนค่าตัวแปรเป็น 0 เพื่อหาจุดตัดแกน x และ y

2x+y = 2 เมื่อแทนค่า x เป็น 0 จะได้ค่า y = 2 ดังนั้นจุดตัดแกน y จะเป็น (0,2)

เมื่อแทนค่า y เป็น 0 จะได้ค่า x = 1 หรือสรุปได้ว่าจุดตัดแกน x เป็น (1,0)

สามารถเขียนกราฟออกมาได้ ดังนี้

2. วิธีการแทนค่าตัวแปร

วิธีนี้จะใช้การหาค่าตัวแปรใดตัวแปรหนึ่ง แล้วจึงนำค่าไปแทนในอีกสมการจนเหลือเพียงตัวแปรเดียว เพื่อหาค่าของสมการนั้น ๆ

ตัวอย่างเช่น

5x – 6y = -4 (สมการที่ 1) และ 3x + 2y = -8 (สมการที่ 2) โจทย์ข้อนี้สามารถจัดรูปสมการที่ 2 ใหม่ออกมาได้เป็น 2y = -8 -3x

y = -1

เมื่อลองแทนค่าทั้ง x และ y ลงในสมการดูแล้ว จะเห็นได้ว่าสมการนี้เป็นจริงนั่นเอง

3. วิธีการกำจัดตัวแปร

กำจัดตัวแปรตัวใดตัวหนึ่งออกไป เพื่อทำให้ค่าสัมประสิทธิ์เท่ากัน จากนั้นดูว่าค่าสัมประสิทธิ์ของตัวแปรนั้นมีเครื่องหมายเหมือนกันหรือไม่ หากเหมือนกัน ให้นำเอาสมการมาลบกัน แต่หากต่างกัน ให้นำเอาสมการมาบวกกัน

ตัวอย่างเช่น

2x + 5y = 20 (สมการที่ 1)

3x+6y =12 (สมการที่ 2)

จะเห็นว่าตัวอย่างข้อนี้มีสมการที่เป็นเครื่องหมายบวกเหมือนกัน ก็นำเอาเลข 3 มาคูณทั้งสองข้างของสมการเพื่อตัดตัวแปร x ออก จะสามารถเขียนสมการได้ ดังนี้

6x + 15y = 60 (สมการที่ 3)

6x+12y = 24 (สมการที่ 4)

ตัดตัวแปร x ออกโดยการลบสมการที่ 4 ออกจากสมการที่ 3 ด้วยการย้ายข้างสมการจะได้

6x+15y-6x-12y = 60-24

ซึ่งจะเท่ากับ

3y = 36 และนำเอา 3 หาร 36 ก็จะได้ค่า y = 12

จากนั้นนำเอาค่า y ที่ได้มาแทนลงในสมการที่ 1 และ 2

2x + 5(12) = 20 หรือ 2x + 60 = 20 จากนั้นทำการย้ายข้างเลข 60 ไปอีกฝั่งของสมการจะได้ว่า

2x = 20-60 หรือ 2x = -40 และย้ายข้างเลข 2 ด้านหน้า x ไปหาร ก็จะได้คำตอบออกมาว่า x = -20

หรือหากแทนค่าลงในสมการที่ 2

3x+6(12) = 12 หรือ 3x+72 = 12 เมื่อย้ายข้าง 72 ไปอีกฝั่งของเครื่องหมายเท่ากับก็จะได้ว่า

3x = 12-72 หรือ 3x = -60 และย้ายข้างเลข 3 ไปหารอีกฝั่งหนึ่งก็จะได้คำตอบว่า x = -20 เท่ากัน

ดังนั้นคำตอบของข้อนี้จึงเป็น (-20,12) นั่นเอง

ตัวอย่างข้อสอบ SAT Math ในหัวข้อระบบสมการเชิงเส้น 2 ตัวแปร

ในส่วนของคำถามในหัวข้อระบบสมการเชิงเส้น 2 ตัวแปรก็จะมีข้อสอบจะเฉลี่ยอยู่ที่ Module ละประมาณราว 2-3 ข้อ คล้ายกับคำถามเรื่องสมการเชิงเส้น 2 ตัวแปร แต่หากข้อคำถามมีความซับซ้อน หรือมีคำว่าระบบ (system) อยู่ในโจทย์ ก็สามารถเดาได้ว่าคำนวนนั้นเป็นหัวข้อของระบบสมการเชิงเส้น 2 ตัวแปร ตัวอย่างคำถาม เช่น

2a + 8b = 198

2a + 4b = 98

The solution to the given system of equations is (a, b). What is the value of b ?

ข้อนี้ตอบ 25 เพราะเมื่อเขียนสมการใช้วิธีการตัดสมการ จะสามารถย้ายข้างสมการและเขียนสมการขึ้นใหม่ได้ว่า (2a-2a)+(8b-4b) = 198-98 หรือ 0+4b = 100 และนำเอาเลข 100 มาหาร 4 ก็จะได้คำตอบว่า b = 25 โดยน้อง ๆ สามารถฝนคำตอบลงใน Answer Sheet ได้เลย

y = 6x+3

One of the two equations in a system of linear equations is given. The system has infinitely many solutions. Which equation could be the second equation in this system?

1. A) y = 2(6x)+3
2. B) y = 2(6x+3)
3. C) 2(y) = 2(6x)+3
4. D) 2(y) = 2(6x+3)

ข้อนี้ตอบ D เพราะข้อนี้มีคำตอบเป็นอนันต์ โดยเมื่อสมการหนึ่งเป็นผลคูณของอีกสมการหนึ่ง สมการทั้งสองจะเทียบเท่ากัน เมื่อคูณทั้งสองด้านของสมการด้วย 2 จะได้ผลลัพธ์ 2(y) = 2 (6x+3) นั่นเอง

3y = 4x + 17

-3y = 9x-23

The solution to the given system of equations is (x, y). What is the value of 39x ?

1. A) −18
2. B) −6
3. C) 6
4. D) 18

ข้อนี้ตอบ D เพราะเมื่อบวกสมการที่สองเข้ากับสมการแรกจะเขียนสมการใหม่ได้ ดังนี้ 3y-3y = 4x+9x+17-23 หรือ 0 =13x-6 เมื่อบวก 6 ทั้งสองข้างของสมการและคูณด้วย 3 ก็จะได้ผลเท่ากับ 18 = 39x นั่นเอง

y = -3x

4x+y =15

The solution to the given system of equations is (x, y). What is the value of x ?

1. A) 1
2. B) 5
3. C) 15
4. D) 45

ข้อนี้ตอบ C เพราะเมื่อแทนที่ค่า -3x ลงไปในสมการที่ 2 จะเขียนสมการใหม่ออกมาได้ว่า 4x+(-3x) = 15 หรือ x = 15 นั่นเอง

ติวเข้มเพิ่มคะแนนสอบ SAT Math ไปกับ House of Griffin

มาถึงตรงนี้หลายคนก็น่าจะพอเห็นภาพของข้อสอบพีชคณิตแบบคร่าว ๆ กันบ้างแล้ว แม้ว่าความจริงข้อสอบ SAT Math ในหัวข้อพีชคณิตจะยังมีข้อสอบอื่น ๆ ที่มากกว่านี้อีก แต่พี่กริฟฟินขอพักเอาไว้ก่อนเพื่อที่น้องแต่ละคนไม่งงจนเกินไป แต่ถ้าใครอยากอ่านเรื่องข้อสอบพีชคณิตกันแบบต่อเนื่อง ก็ไปต่อกันที่ Part 2 เลย ที่สำคัญ เวลาทำสอบอย่าลืมอ่านและทบทวนโจทย์ดี ๆ เพื่อที่จะได้ไม่พลาดคะแนนสำคัญไปก็อ่านเพิ่มเติมได้ที่ คลิก

ส่วนใครที่อ่านแล้วยังงงอยู่ หรือรู้สึกว่าตัวเองไม่ถนัดการทำข้อสอบในรายวิชาคณิตศาสตร์และอยากได้ผู้ช่วยติวสอบก็สามารถทักมาปรึกษาพี่กริฟฟินเพื่อลง คอร์สติว SAT Math กับผู้เชี่ยวชาญตัวจริงได้เลย รับรองว่าติวเข้มแบบเน้นทุกหัวข้อ แถมยังมีพี่ทีมงาน House of Griffin คนอื่น ๆ คอยช่วยเหลือตอบคำถามและข้อสงสัยเพิ่มเติม เพื่อเตรียมตัวสมัครสอบกันได้เลย คลิก